A commonly encountered type of inverse problems is to estimate coefficient functions of a
partial differential equation over a domain based on measurements of its solutions either inside
or at the boundary of the domain. The computational treatment of such problems requires
discretization of the problem, e.g., by using the finite element method. The discretization process
generates a modeling error, and if not properly analyzed, the error can be detrimental due to the
ill-posedness of the inverse problem in which small errors in data propagate to huge errors in the
solution, see Figure. This project addresses the question by recasting the inverse problem in a
novel way, where the discretization is part of the inverse problem. The methodology is based on
hierarchical Bayesian modeling of the discretization and the modeling error. The methodology
will be developed to address selected biomedical imaging applications.

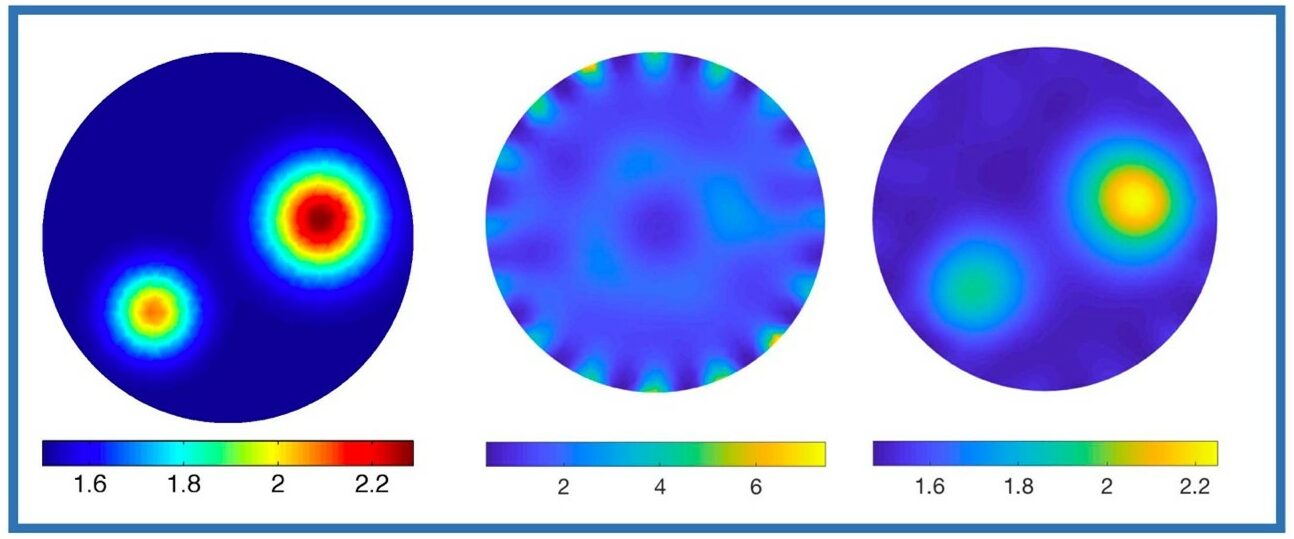
A computed example of the effect of a discretization error in electrical impedance tomography,
where the goal is to estimate the electric conductivity distribution inside a body from
current/voltage measurements at the boundary.: Left: True conductivity distribution used to
generate synthetic data. Middle: Reconstruction using a coarse mesh without the modeling error
analysis. Right: The reconstruction using the same coarse mesh with careful modeling of the
discretization error.

Bridging the gap between discrete and continuous PDE in medical imaging

NSF- DMS 2204618 Project Awarded to Erkki Somersalo, PI. $299.998. 8/1/2022 – 7/31/2025.